A refractometer is one of the most useful tools a brewer can have. It allows for near-instantaneous measurements of specific gravity, without having to compensate for or adjust sample temperature or withdraw a large volume of wort/beer (a significant concern at homebrew scales). There are a few issues associated with accurately using a refractometer for brewing, though. First, a refractometer does not actually measure specific gravity, or sugar content. Instead it simply projects a line through a reticle, and relies on the fact that the refractive index of the fluid will move a line up and down the reticle. For a simple sucrose solution (the refractometers common to homebrewers are “borrowed” from the wine industry) the refractive index depends only on the sugar content and the temperature. Automatic temperature correcting (ATC) refractometers use a bimetal strip to cancel out the temperature variable (within a given range), meaning that the reticle can be marked directly in units of sugar content. Brewers’ wort, however, is not a sucrose solution, and so a “wort correction factor” must be applied. Generally this is done by dividing the refractometer reading by 1.04.
The second, more intractable problem with using a refractometer to determine specific gravity is that once fermentation begins, the beer becomes a three-part solution: sugars, water, and alcohol. There is no longer fidelity of measurement – that is to say, there can be more than one specific gravity that will correlate to the same refractive index. Generally speaking, however, only one of the potential data points will be sensible for a real beer. Making that assumption, it should be possible to develop a correlation between the measured refractive index and the actual gravity of the beer, as long as the alcohol content can be estimated. This means that if both pre- and post-fermentation readings are taken, the FG can be predicted. Various software packages and websites incorporate tools to do just that, all of which seem to use the same correlation:
FG = 1.001843 – 0.002318474*RIi – 0.000007775*RIi² – 0.000000034*RIi³ + 0.00574*RIf + 0.00003344*RIf² + 0.000000086*RIf³
Where RIi and RIf are the initial and final refractive indices, respectively, in wort-corrected degrees Brix.
I took pre- and post-fermentation readings of ten beers, with OGs ranging from 1.036 to 1.103, using both a refractometer and hydrometer. In every case the refractometer correlation provided an FG that was lower than the hydrometer reading, by anywhere from 0.5 to 8.5 “gravity points” (1000*(SG-1)). The mean discrepancy is 5.1 points. The main variable of concern seems to be the attenuation of the beer; the greater the attenuation, the larger the discrepancy. The results are plotted below.
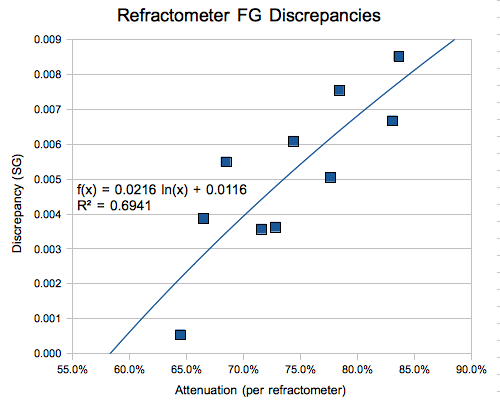
Note that the discrepancy is zero at about 58% attenuation (71% apparent attenuation). I have no information on who originally developed the correlation, but my supposition is that they only tested worts with about this degree of fermentability. A logarithmic curvefit provides a reasonably good (R² ≅ 0.7) approximation for the offset that is needed; by adding this correction factor to the standard correlation, the maximum discrepancy for this dataset is reduced to only 2.1 points, and the average to 0.1 points. Unfortunately, the resulting equation is a bit unwieldy:
FG = (1.001843 – 0.002318474*RIi – 0.000007775*RIi² – 0.000000034*RIi³ + 0.00574*RIf + 0.00003344*RIf² + 0.000000086*RIf³) + 0.0216*LN(1 – (0.1808*(668.72*(1.000898 + 0.003859118*RIi + 0.00001370735*RIi² + 0.00000003742517*RIi³) – 463.37 – 205.347*(1.000898 + 0.003859118*RIi + 0.00001370735*RIi² + 0.00000003742517*RIi³)²) + 0.8192*(668.72*(1.001843 – 0.002318474*RIi – 0.000007775*RIi² – 0.000000034*RIi³ + 0.00574*RIf + 0.00003344*RIf² + 0.000000086*RIf³) – 463.37 – 205.347*(1.001843 – 0.002318474*RIi – 0.000007775*RIi² – 0.000000034*RIi³ + 0.00574*RIf + 0.00003344*RIf² + 0.000000086*RIf³)²))/(668.72*(1.000898 + 0.003859118*RIi + 0.00001370735*RIi² + 0.00000003742517*RIi³) – 463.37 – 205.347*(1.000898 + 0.003859118*RIi + 0.00001370735*RIi² + 0.00000003742517*RIi³)²)) + 0.0116
In order to spare anyone who might be interested some trouble, I’ve put together a simple spreadsheet that will calculate FG using both the old and new correlations, in addition to attenuation and ABV. If you end up using it for a significant number of batches, please share your results.
Update: 20 July 2010
I’ve since refined the FG correlation, using a more mathematically rigorous method. I leave the original post up for transparency’s sake, but if you’re looking for an FG calculator, please check out the new post.
Update: 07 Apr 2011
I’ve tweaked the correlation and posted some results from other brewers, as well as an updated spreadsheet: Refractometer FG Results
Spreadsheet download:
fg_calculator.ods | fg_calculator.xls
I’m trying to square this with Papazian’s zen mantra “relax, don’t worry, have a homebrew”, but my brain keeps shorting out.
Yeah, there’s definitely no way to square this kind of thing with the RDWHAHB mindset. What can I say? I’m a scientist; if my instruments aren’t calibrated, I’m not happy.
‘a bit unwieldy’ ??? LOL! I’m surprised Excel allowed a formula that long!
But is there a prob with the ABV part? I was just messing around with it and changing number in the brix section, the ABV always seems to be 5.0% or 4.9% I tried brix # of Original always 13 and final of 1,3,5,7,9,11, and 13.
But I’m more interested in the brix to SG number anyways.
Thanks for the catch, Dave. I forgot to convert the FG to °Plato in the ABV formula. I’ve uploaded a new version that should work correctly.
[...] decided to use this one: http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ He goes into the typical formula and its margin of error. Then proceeds to work out a better [...]
[...] stopped. I found this for the calc. It seems more acurate then most, and he briefly explains why. http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ __________________ Primary: Dropkick Red Primary: Bubba Mustafa's Plan B Bottled: Basic Red [...]
[...] NoNothing said, you can apply a correlation to approximate the FG. I did some analysis recently (Refractometer Estimates of Final Gravity) and found that while the default correlation isn't very good, I can add an offset to improve its [...]
[...] Refractometer CorrelationRegulating Fermentation TemperaturesWater, Water EverywhereTHA CloningRefractometer Estimates of Final GravityMore [...]
[...] various programs do include calculations for your refractometer to work with fermented wort but here is a link for a better calculation. I have been using this and comparing it to my hydrometer and it seems [...]
[...] Here is a article and a program that works better then the old standard for calculating FG using a refractometer. I have used this with over 10 different beers and compared to my hydrometer and it has been within a point everytime. http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ [...]
[...] I'm waiting for the fallout from his data analysis before I continue doing this. Great work sean! http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ __________________ She was only a whiskey maker, but he loved her [...]
Hi Sean,
The original formula is also borrowed from wine-making; when making wine I find the formula to be spot on generally.
neets
That makes sense, since in any wine must very nearly 100% of the sugars would be fermentable. Thanks.
Sean
[...] To check your refractometer, calibrate first with distilled water to read zero. Then add 10gm sugar to 90gm warm water and dissolve. This mixture should give you a reading of 10 brix, approx 1.040 gravity. If it is off then it is your refractometer. If it is correct I would suspect your hydrometer. Also below is a link to the best spreadsheet I have found for calculating FG. All other programs I have used (morebeer, beersmith, etc.) start to give inaccurate readings when attenuation starts getting close to the 80% mark. http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ [...]
[...] Refractometer CorrelationYeast Pitching Rate ResultsBuild a Better StirplateOf Ice and 10°PRefractometer Estimates of Final GravityTHA CloningAeration and Yeast StartersYeast Ranching and YouTwo-Stage Starter CalculationsRegulating [...]
[...] some more info: http://seanterrill.com/2010/06/11/refractometer-estimates-of-final-gravity/ http://seanterrill.com/2010/07/20/toward-a-better-refractometer-correlation/ [...]
Thanks for a deep analysis Sean, I’m surprised the simple linear forumula gives such good results!
I created a simpler spreadsheet to use for my daily brewing needs that doesn’t have the “extra” columns and using your new linear formula. Since my refractometer does auto-temperature correction and has a SG and brix scale, I read mine off in SG. This spreadsheet simplifies that a little for a single beer read multiple times. It’s based from one from morebeer.com that I liked, but heavily modified using the improved formulas, etc.
http://www.brettanddebbie.com/blog/archives/beer/refract_blank.xlsx
I thought I’d post it here in case others find it useful.
Thanks Brett. The spreadsheet looks nice, although it doesn’t seem to work in OpenOffice. Bear in mind, though, that unless there’s a new one on the market, those SG refractometers were manufactured incorrectly. They used an approximation, SG = 1 + 0.004*Bx, rather than converting correctly. The approximation is only within one gravity point for SGs below ~1.055.
I noticed that you read Cryptonomicon recently. That’s probably my favorite book.
Cheers,
Sean
Sorry about the Microsoft specific format, and thanks for the reply, I had not heard of this defect. Mine was bought a few months ago and I recall the manufacturing date being a maybe a year or two old. I suppose I should read off the Brix scale instead? You seem to understand a lot about refractometer precision..!
I guess this gives me a couple more changes to make to my spreadsheet..
It’s easy to check if your SG scale is accurate; just look at the line for 20°Bx. It should correspond to about 1.084 SG. If it’s ~1.080 instead, then the manufacturer didn’t apply the correct conversion.
Sean
Wow, Sure enough it’s a bad conversion. Looking across from 20Bx I see 1.078 or so. Thanks for the tip!
[...] [...]
Sean:
I don’t think I understand why you plotted the discrepancy vs attenuation by refractometer instead of discrepancy vs attenuation by hydrometer. It seems more intuitive that one would want to look at the discrepancy relative to a value that is not so sensitive to the alcohol content of the beer., i.e., the attenuation based on the hydrometer values. I suppose mathematically they are related, but the figure seems to create the appearance of an infinite loop. (Discrepancy of final gravity is dependent on the value of the refractometer-based gravity which is itself dependent on the extent of the discrepancy.)
Fred,
To be honest, I’m not sure. I’d like to think there was a reason, but it’s been almost two years and I just don’t remember. For what it’s worth, I did a curvefit using the actual attenuation and it was almost identical.
Sean
[...] are of course a whole other story, that I won’t be getting in to, instead have a look at this and [...]
Hi Sean,
As I recently purchased a MoreBeer refrac, I was researching how to use them during and after fermentation. I immediately downloaded a widely available spreadsheet, noticed the old cubic regression, and began to wonder who developed the relationship and how many measurements were used to develop it. Some use of the google machine then landed me here. I just read your three (I think) posts on the subject and you walked through the exact thought process I would have taken to answer my own questions. Thanks so much for the thorough documentation and for providing this spreadhsheet and php tool. I now have a better understanding of how this process works and of the accuracy and precision I can expect from this new toy. Thanks!
[...] BeerSmith or the web based calculator at onebeer) and plenty of information about it, for example here. The refractometer is less breakable, easier to read, only uses 1 drop of wort (so reduces the [...]